The following is an excerpt from a group project completed in my finial year at the University of Aberdeen. Dr. Kaliyaperumal Nakkeeran supervised the project. The group project title was Simulation of Pulse Propagation in Optical Fiber Transmission Systems. The aim of the project was to simulate the pulse propagation in dispersion managed (DM) optical fiber transmission systems. Effects like optical losses, group-velocity dispersion and self-phase modulation are analyzed in this project. Part of my contribution to the project was the production of a MATLAB simulation of the pulses’ propagation through the wave-guide.
Introduction
The aim of this group project was to simulate the pulse propagation in dispersion managed (DM) optical fibre transmission systems. Effects like optical losses, group-velocity dispersion and self-phase modulation are analyzed in this project.
Nonlinear pulse propagation in a fiber can be described by the generalized nonlinear Schrödinger equation (NLSE), which has the form,
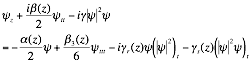
Wwhere ψ(z, t) is the slowly varying envelope amplitude of the electric field measured in units of square root of Watts at position z, at time t. Subscript z or t denotes the partial derivative with respect to that letter. β2(z) and β3(z) represent the second and third order dispersion coefficients respectively. γ(z) represents the strength of the nonlinearities.
Split Step Fourier Method
Description
The non-linear Schrödinger equation describes the propagation of the wave through an optical wave-guide. The equation is described in Equation 2‑1. The equation represents the non-linear response of the dielectric to the electric field of the propagating light wave.
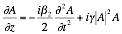
The non-linear Schrödinger equation consists of two main components, the linear component as described in Equation 2‑2 and the non-linear component as described in Equation 2‑3. The non-linear and the linear components of the equation is solvable separately however non-linear Schrödinger equation does not have a simple solution.
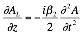
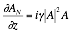
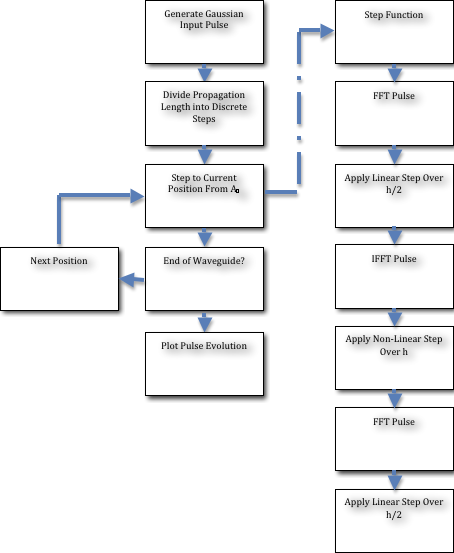
If the only a step h is taken along the waveguide z, then the linear and non-linear components can be treated separately resulting in only a small numerical error. These steps are illustrated in Figure 2‑1.

In each step in the splits-step method there are three operations, involving the non-linear and linear components. The non-linear transfer function is applied from ![]() to
to ![]() , then from
, then from ![]() to
to ![]() . The linear transfer function is then applied from
. The linear transfer function is then applied from ![]() to
to ![]() . This is illustrated in Figure 2‑2.
. This is illustrated in Figure 2‑2.

Derivation
Linear Component
The linear component of the operation can be obtained from the non-linear Schrödinger’s equation (Equation 2‑4).
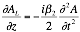
The second derivative of the amplitude can be substituted with the Fourier transform as described in Equation 2‑5,
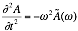
Rearranging for ![]() gives Equation 2‑6,
gives Equation 2‑6,
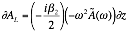
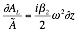
Integrating ![]() with respect to
with respect to ![]() between
between ![]() and
and ![]() , and
, and ![]() with respect to
with respect to ![]() over o to h as in Equation 2‑8,
over o to h as in Equation 2‑8,
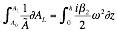
giving Equation 2‑9.
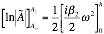
Re-arranging into a transfer function between the current step and the next step values as in Equation 2‑11,
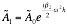
When implemented in MATLAB Equation 2‑11 takes the form:
i = sqrt(-1);
A = A.*exp(-alpha*(h/2)+i*beta/2*w.^2*(h/2));
Non-Linear Component
The non-linear component of the operation can be obtained from the non-linear Schrödinger’s equation (Equation 2‑12).
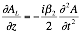
The equation is then rearranged in terms of ![]() , as in Equation 2‑13
, as in Equation 2‑13
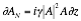
Integrating ![]() with respect to
with respect to ![]() between
between ![]() and
and ![]() , and
, and ![]() with respect to
with respect to ![]() over 0 to h as in Equation 2‑14,
over 0 to h as in Equation 2‑14,
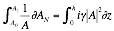
giving Equation 2‑15
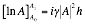
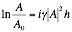
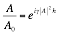
Re arranging into a transfer function between the current step and the next step values as in Equation 2‑18,
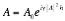
When implemented in MATLAB Equation 2‑18 takes the form:
i = sqrt(-1);
A = A.*exp(i*gamma*(abs(A).^2)*h);
Demonstration of Algorithm
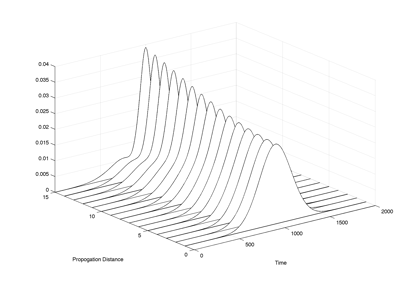
The MATLAB program is demonstrated in Figure 2‑2. In this graph a generic pulse is shown evolving as it propagates through a glass wave-guide.
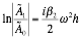
23 replies on “Pulse Propagation Modeling in Dispersion Managed Optical Fibers”
can i have the complete code
please send me : code simulation Matlab for NLSE
excellent description. thanks.
thanks for your description.
Hi, I am Dr. Hamie from the lebanese University, I am wondering if could you send to me your MAtlab code.
Thanks a lot in advanced.
Hi Dr. Hamie,
Can I have the matlab code.
Regards.
can I have the matlab codes for this.
tahnks for this page it also helped me alot.
Hello,
I would be very interested to see the MATLAB code for this
Cheers
Hi,
Could you send me the matlab code please?
That’s gonna be very much appreciated.
Can I have matlab code please
regards
Thank you for the good work. Would you please share the matlab code with me?
Best Regards.
Abou
Hi,
Could you send me the matlab code please?
thank’s very much
Hello
I like your work, could you plesae share the matlab code with me?
please
Thank’s
can have the full code?
thanks this was an excellent description.
hi,
can i try your code. I am interested to know Is there an flexibility to define w-index profile in the code .
Thank you in advance,
Hello, been trying to create something similar myself, results are not of a soliton but more of a soliton lumped, could it be possible for you to show your code in it’s entirety or to send it?
Thank you very much.
please can anyone send me : the complete matlab code for simulation for NLSE..its really urgent for me
If possible could you please mail me your matlab code.This is a part of my topic of research and will help me a lot
Could you send me the matlab code, please?
Hello!
Could you send me the matlab code please?
Hello, kindly share your matlab code with me
Excellent work! Kindly share your code with me please.
i like ur work.. could you plz share the matlab code for the same