This entry will detail the geometry of multi-static passive RADAR and describe how it obtains a target solution. For this report, a multi-static passive TDOA RADAR configuration will consist of a single receiving station that monitors for direct signals from the transmitters and indirect, multi-path signals reflected from potential targets. Other configurations are possible but the two-dimensional solution described here requires three transmitter-receiver combinations. To obtain a target the system measures the time difference of arrival (TDOA) of the multi-path signal is compared to the direct path signal from the same transmitter. Solutions for possible targets are calculated using the measured TDOA timings.
Bi-static RADAR geometry
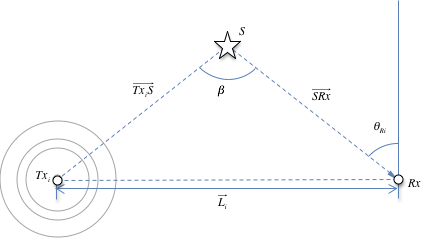
Figure 1 illustrates a simple bi-static RADAR system consisting of a transmitter
, a target 
and a receiver 
. A distance separates the transmitter and receiver 
. The sum of the distances between the target 
and the transmitter 
and the distance between the target and receiver 
is the range of the bi-static RADAR. Equation 1 shows how the bi-static range 
can be determined by measuring the time difference of arrival 
of the reflected path signal via the target relative to the direct path signal 
.
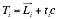
Where 
is the speed of propagation of the signal through air.
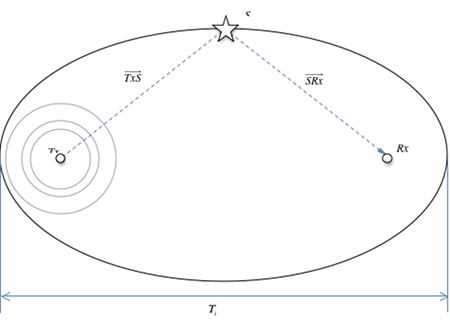
Knowing the bi-static range allows the target to be positioned somewhere on an ellipse with the receiver and transmitter as foci. The sum of the distances from the points of the ellipse to the transmitter and receiver is equal to the bi-static range 
.
Equation 2 also demonstrates this relationship.
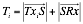
The location of the transmitter 
is at 
. The location of the receiver 
is at 
and the target is located 
. Expanding Equation 2 gives
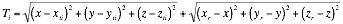
Multi-Static Radar Geometry
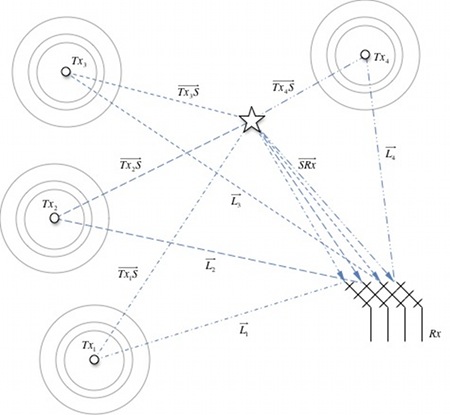
Figure 3 shows a multi-static system consisting of four transmitters, a target and a receiver. There is a direct path signal ,
from every transmitter to the receiver. A multi path signal from each of the transmitter 
is reflected by the target 
and is intercepted by the receiver. The path the reflected signal follows from the target to the receiver is common for all transmitters 
.
2D Operation
A two dimensional solution for the target can be calculated using measurements of the TDOA of the reflected signal relative to the direct signal from each transmitter. The 2D solution requires three TDOA measurements from three transmitters 
, 
and 
. Using the TDOA values and the known locations of the transmitters Equation 3 can be rewritten for each transmitter
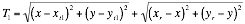
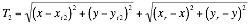
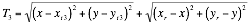
Equation 4 and Equation 5 can be rearranged into;
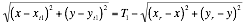
and
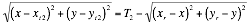
Squaring both sides of Equation 7 and Equation 8 gives
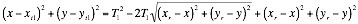
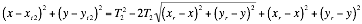
Rearranging Equation 9 and Equation 10 in terms of 
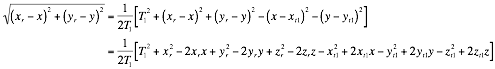
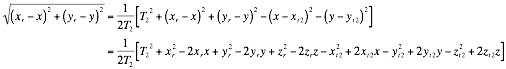
Equating Equation 11 and Equation 12 gives
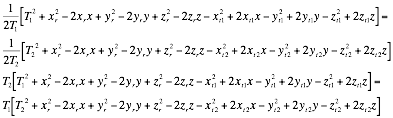
Rearranging Equation 0‑10 in the form of
Equation 14
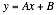
gives
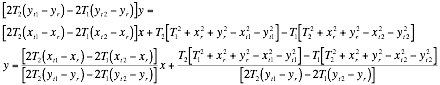
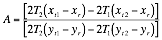
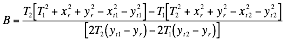
Using Equation 4 and Equation 6 rearranging into the form
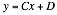
gives
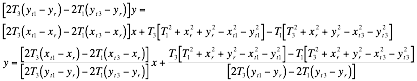
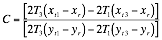
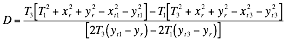
Equating Equation 14 and Equation 18
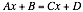
and rearranging for
gives
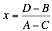
Subtitling
into Equation 14 for
gives
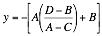
The next post will expand the 2D derivation into a solution in 3D, the extra dimension added using an additional transmitter. The concept of a geometric error will also be introduced.